# install.packages("COGARCH", repos="http://R-Forge.R-project.org")Software development
R packages
- sBF: Smooth Backfitting
- parsec: Partial Orders in Socio-Economics
- ineqJD: Inequality Joint Decomposition
- POSetR: Partially Ordered Sets in R
- HOasso: Higher Order Assortativity for Complex Networks
- COGARCH: Simulation and parameters estimation for COGARCH(1,1) processes with different methods
R Programming Examples
Zenga inequality curve decomposition
ineqJD package required
library(ineqJD)Data simulation
set.seed(23)
n <- 10^4
# vector denoting group membership
G <- sample(1:3, n, replace = TRUE)
# vector of the first source
X1 <- rexp(n)
# vector of the second source
X2 <- rlnorm(n)
data <- data.frame(G, X1, X2)Decomposition
x <- dataProcessing( # data preparation
units = data[, c('X1', 'X2')],
groups = data[, 'G'],
)
decomposition <- zenga(x)
ic <- inequalityCurves(decomposition)
contrib1 <- inequalityCurves(decomposition, l = 1)
contrib12 <- inequalityCurves(decomposition, l = 1:2)Graphical representation
plot(ic, pch = NULL, lwd = 2)
plot(contrib1, add = TRUE, pch = NULL, lwd = 2, col = 2)
plot(contrib12, add = TRUE, pch = NULL, lwd = 2, col = 3)
text(0.1, 0.1 + 0:2/3, labels = c("G1", "G2", "G3"))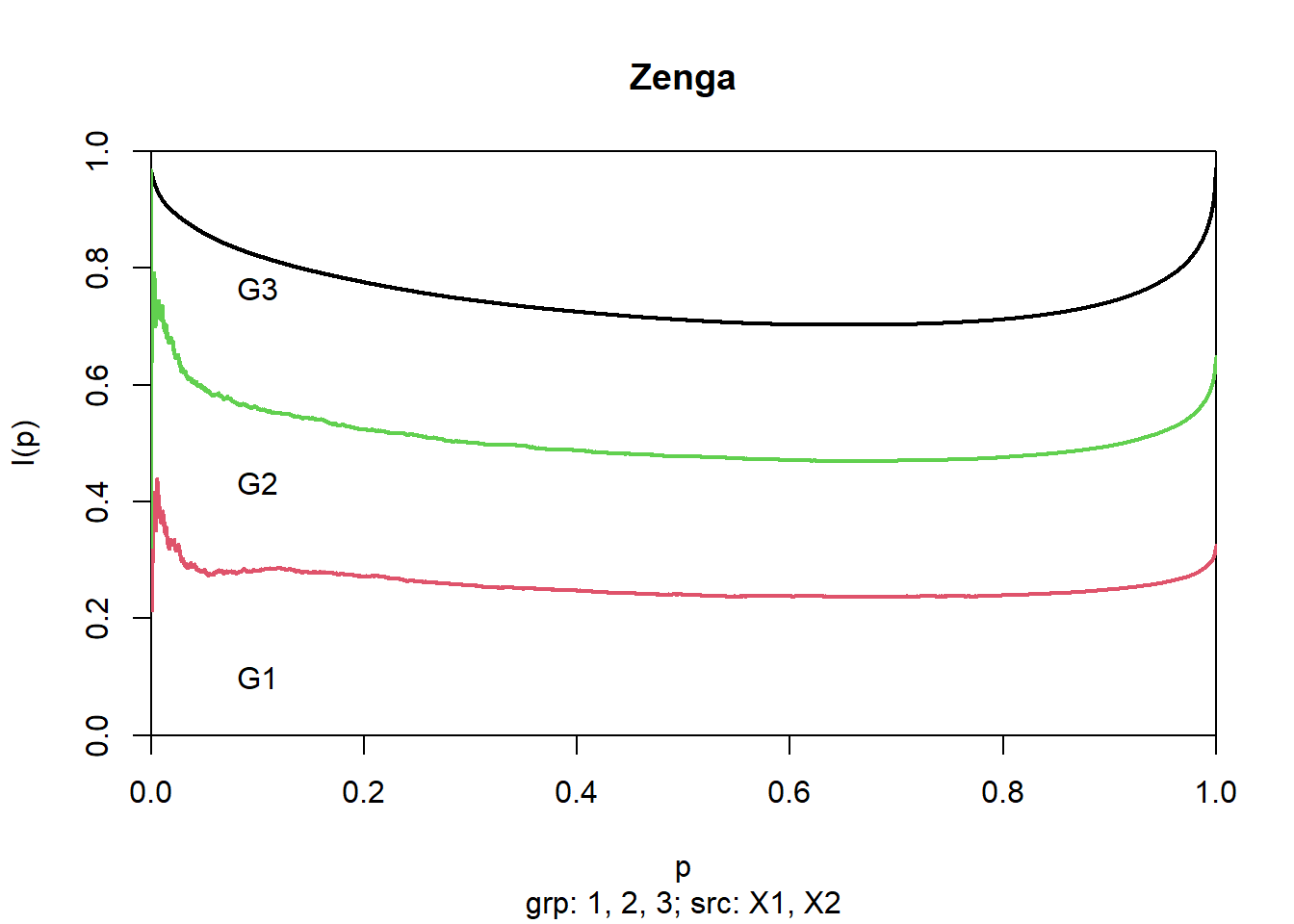
Higher Order Assortativity
Here a simplified description of Higher Order Assortativity assortativity is is shown. In case of undirected and unweighted graphs, assortativity of order \(h=1\) is the correlation between the degrees of adjacent nodes.
igraph package required
library(igraph)Network creation from adjacency matrix
n <- 5
V <- LETTERS[1:n]
A <- matrix(c(
0, 1, 1, 0, 0,
1, 0, 1, 0, 0,
1, 1, 0, 1, 0,
0, 0, 1, 0, 1,
0, 0, 0, 1, 0
), nrow = n,
dimnames = list(from = V, to = V)
)
N <- graph_from_adjacency_matrix(A, mode = "max")
plot(N, vertex.color = "white")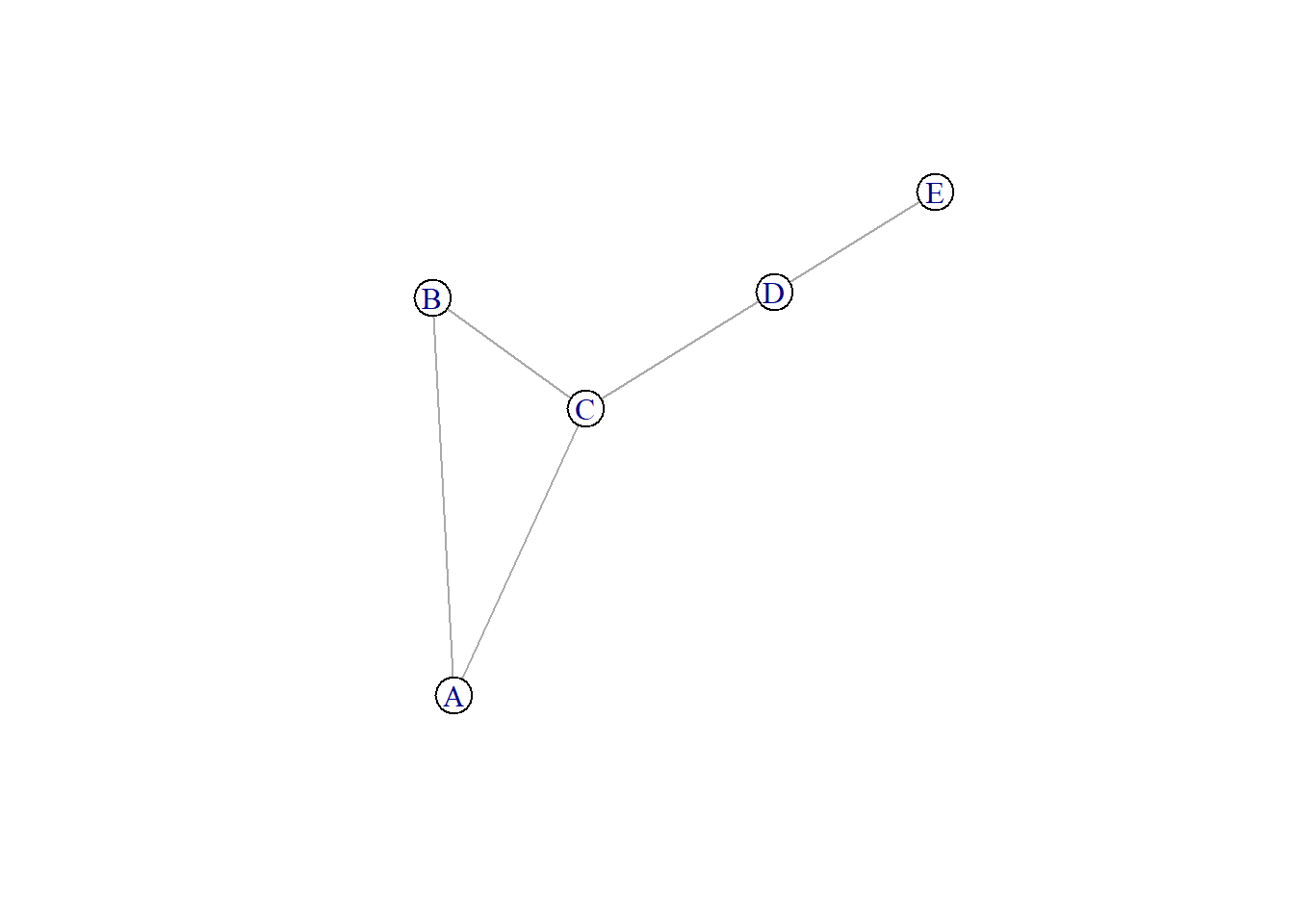
Degree as \(\mathbf{d} = \mathbf{A1}\) centrality measure.
d <- degree(N); dA B C D E
2 2 3 2 1 Function to evaluate degree-covariance between joint vertices \[ \text{Cov}(\mathbf{d}, \mathbf{A}) = \mathbf{d}^\top\left(\mathbf{E}-\mathbf{q}\mathbf{q}^\top\right)\mathbf{d} \] where \(\mathbf{E} = \frac{\mathbf{A}}{\|\mathbf{A}\|_1}\) is the relative adjacency matrix and \(\mathbf{q} = \mathbf{E1}\) is the relative degree vector
Cov <- function(d, A) {
E <- A / sum(A)
q <- rowSums(E)
d %*% (E - outer(q, q)) %*% d
}
Cov(d, A) [,1]
[1,] -0.04Assortativity index \[ \rho = \frac{\text{Cov}(\mathbf{d}, \mathbf{A})}{\text{Cov}(\mathbf{d}, \textbf{D}_\mathbf{d})} \] where \(\textbf{D}_\mathbf{d}\) is the diagonal matrix with \(\mathbf{d}\) on the main diagonal
Cov(d, A) / Cov(d, diag(d)) [,1]
[1,] -0.1111111Higher order relative adjacency matrix \[ \textbf{E}_h = \textbf{D}_\mathbf{q} \textbf{P}^h \] where \(\textbf{D}_\mathbf{q}\) is the diagonal relative degree matrix and \(\textbf{P}\) is the row-stochastic matrix of the adjacency matrix. If there are not isolated nodes
E <- A / sum(A)
q <- rowSums(E)
D <- diag(q)
P <- solve(D) %*% E
round(P, 3) to
A B C D E
[1,] 0.000 0.500 0.5 0.000 0.0
[2,] 0.500 0.000 0.5 0.000 0.0
[3,] 0.333 0.333 0.0 0.333 0.0
[4,] 0.000 0.000 0.5 0.000 0.5
[5,] 0.000 0.000 0.0 1.000 0.0rowSums(P)[1] 1 1 1 1 1Matrix-power recursive function
matrixPower <- function(M, h) {
if (h == 1)
return(M)
return(M %*% matrixPower(M, h - 1))
}Assortativity of order \(h = 3\)
P3 <- matrixPower(P, 3)
round(P3, 2) to
A B C D E
[1,] 0.17 0.29 0.38 0.08 0.08
[2,] 0.29 0.17 0.38 0.08 0.08
[3,] 0.25 0.25 0.17 0.33 0.00
[4,] 0.08 0.08 0.50 0.00 0.33
[5,] 0.17 0.17 0.00 0.67 0.00rowSums(P3)[1] 1 1 1 1 1E3 <- D %*% P3
round(E3, 2) to
A B C D E
[1,] 0.03 0.06 0.08 0.02 0.02
[2,] 0.06 0.03 0.08 0.02 0.02
[3,] 0.07 0.07 0.05 0.10 0.00
[4,] 0.02 0.02 0.10 0.00 0.07
[5,] 0.02 0.02 0.00 0.07 0.00Cov(d, E3) / Cov(d, diag(n)) [,1]
[1,] 0.025asrt <- Vectorize(
function(h)
Cov(d, D %*% matrixPower(P, h)) / Cov(d, diag(n))
)
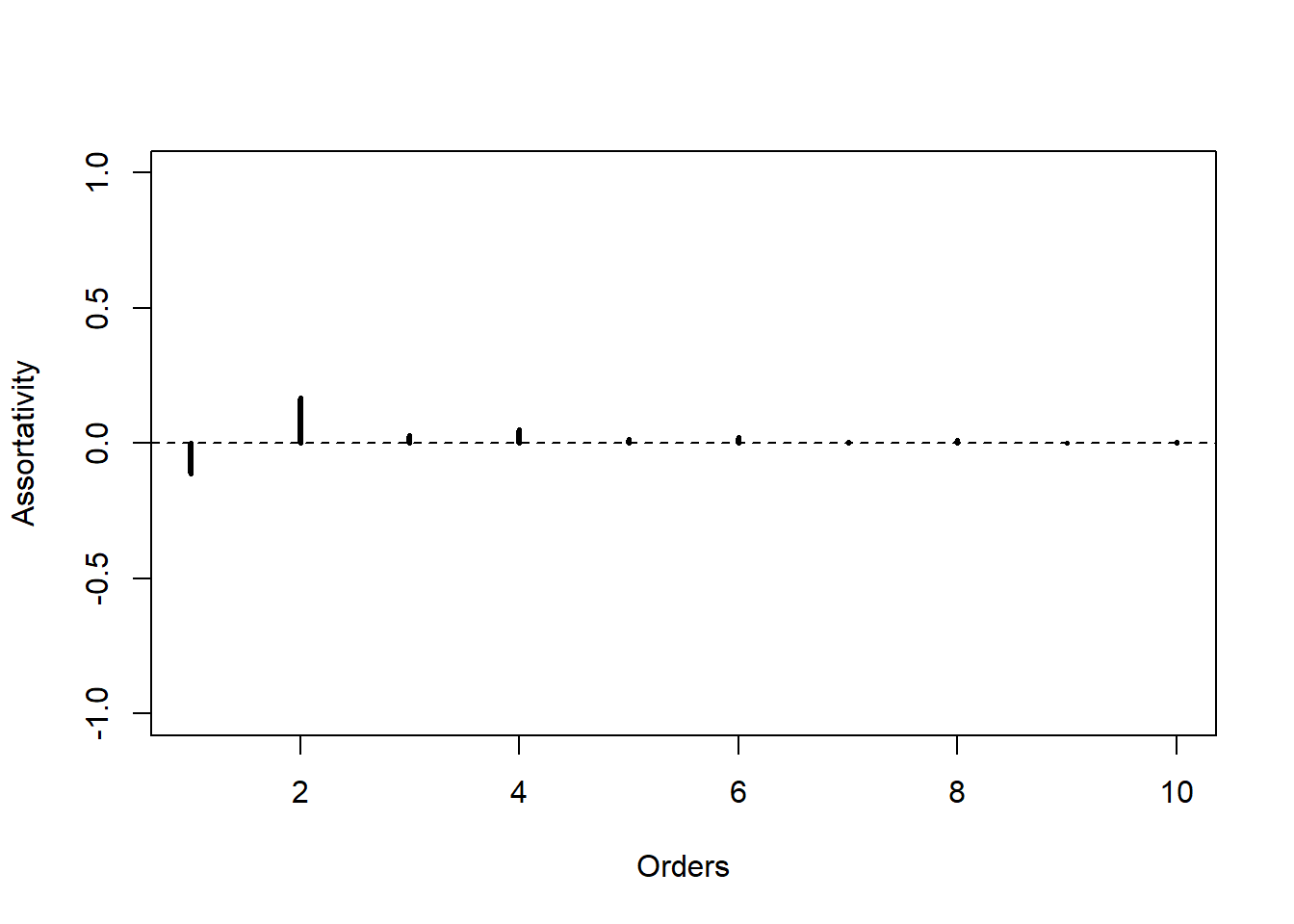
plot(asrt(1:10), type = "h", xlab = "Orders",
ylab = "Assortativity", lwd = 3, ylim = c(-1, 1),
panel.first = abline(h = 0, lty = 2)
)
Using HOasso package
The package allows the evaluation of Higher Order Assortativity for digraphs and weighted graphs too, but in this case we refer to the previous example, undirected and unweighted, in order to show how to get the same results using only one function.
library(HOasso)a <- HOasso(N, h = 10)
class(a)[1] "assortativity" "numeric" The result is an object of class assortativity with its own methods but it inherits the properties of numeric vectors.
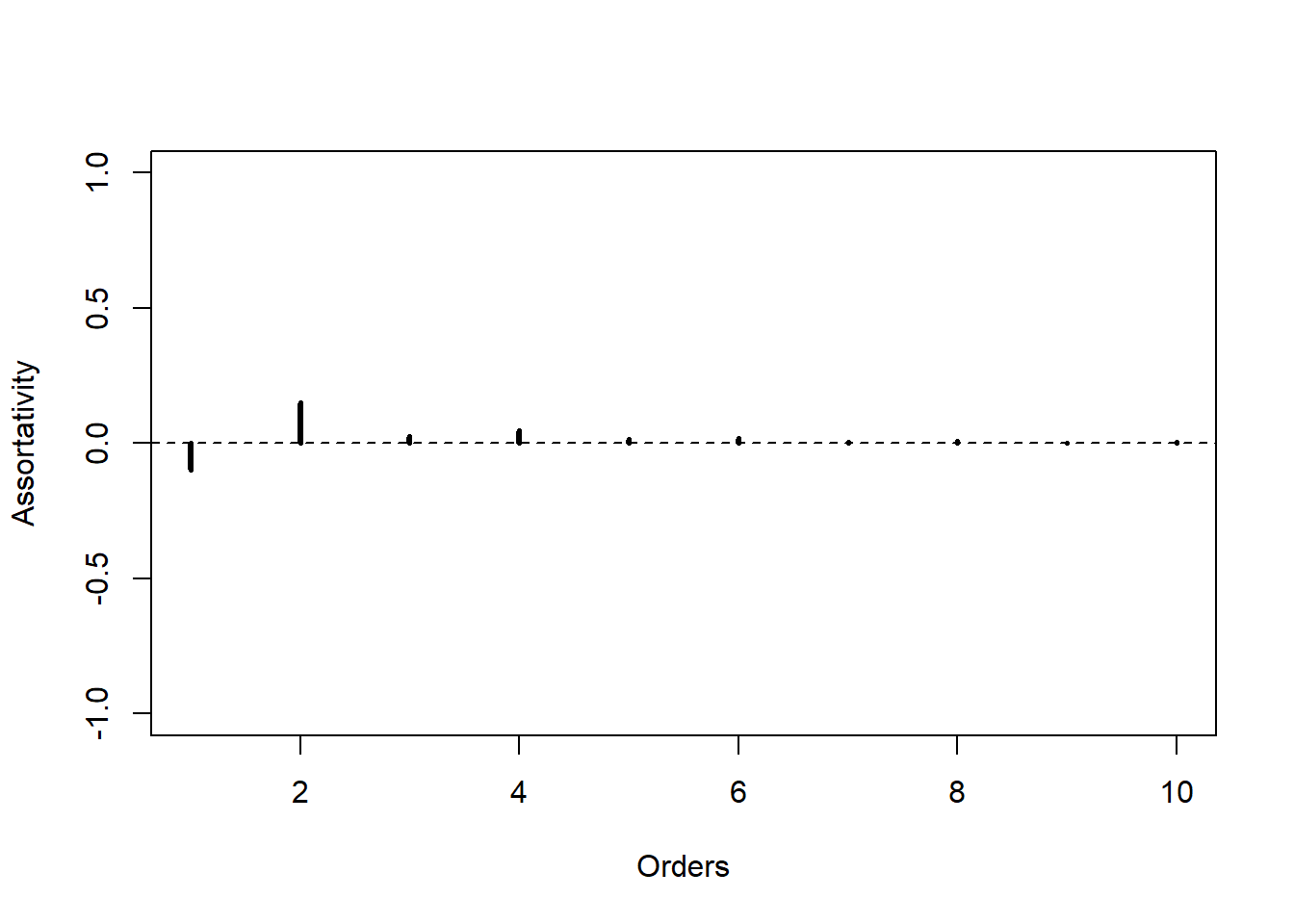
print(a)
order assortativity
1 -0.111111111
2 0.166666667
3 0.027777778
4 0.050925926
5 0.016203704
6 0.021990741
7 0.005594136
8 0.010898920
9 0.001012731
10 0.005875450plot(a, lwd = 3, panel.first = abline(h = 0, lty = 2))